
Unknot Diagrams: The Art and Magic of the Trivial Knot

Peter Prevos |
2129 words | 10 minutes
Share this content
One of my biggest frustrations with watering the garden is that the hose always seems to be knotted. No matter how careful I am coiling it when done, knots seem to be everywhere where you don’t want them — garden hoses, headphone wires, extension cords or even your muscles. However, these knots are just an illusion most of the time, and my hose is merely a complex’ unknot’, as mathematicians would say.
Mathematicians study knots in great detail. Not to prevent their garden hoses from becoming a tangled mess but to better understand reality. For example, this branch of mathematics provides insight into the structure of DNA and entanglement in quantum mechanics and the behaviour of fluids. But knots can also be beautiful and a fascinating object of study by itself.
The unknot, also known as the trivial knot, is the most simple knot. In its simplest form, it is just a loop but with hidden complexity. The unknot is deceptive because what looks like a knot is actually not a knot. Mathematicians have designed complex unknots to study their properties. The unknot has also inspired painters as works of art. Lastly, magicians have developed methods to create unknots that look like real knots.
This article is an ode to the trivial knot and contains a gallery of mathematical, artistic and magical unknot diagrams.
The Unknotting Problem
Knot theory is a young branch of mathematics that started about a century ago. A mathematical knot is not the same as a knot in the real world. Instead, mathematical knots are closed loops in three-dimensional space. The loops need to be closed to ensure that their properties stay the same when we deform them. Mathematicians have defined thousands of knots and analysed their properties. The image below shows the first four basic knots.

The unknot is a closed loop that is not knotted. This is a convoluted way of saying that an unknot is a circle. Although this description is as simple as possible, it is not always that clear whether a loop is knotted or just a ring. The diagram below shows two examples that are indisputably not knotted.

One of the fundamental and most challenging problems in knot theory is the unknotting problem. While in the physical world, you would simply pull the string to test its knottedness, we require a more rigorous and reproducible process in the abstract world of mathematics. The example below looks like a proper knot, but you’ll see that it is just a loop when you create one from a piece of string.

The unknotting problem is deceptive because complex projections of the unknot look like genuine knots. Mathematicians have developed a plethora of systematic methods to test whether a tangled loop is an actual knot or merely a trivial one.
Reidemeister Moves
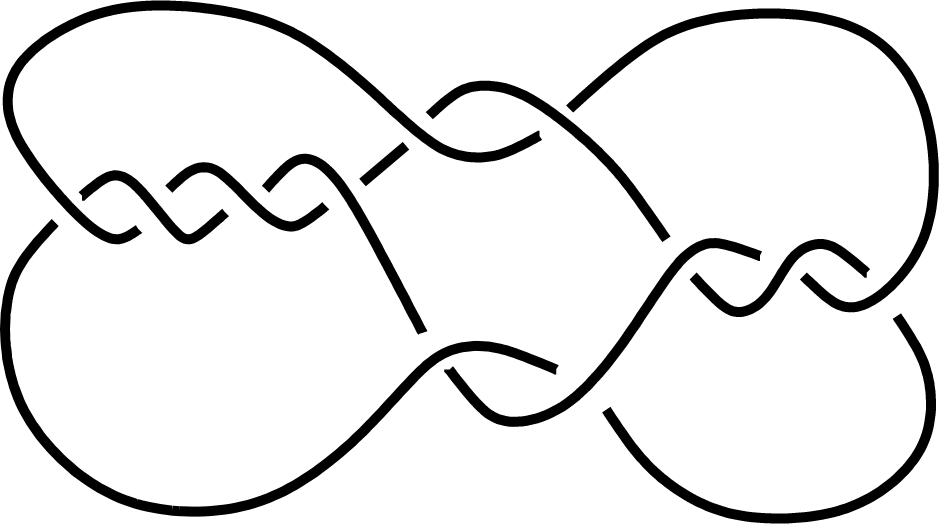
The Reidemeister moves are the oldest test of whether a knot is trivial. This is a set of three allowed changes to a knot to transfer it from one state to the next. A sequence of these moves is proof that a knot is really an unknot.
The diagram below shows how to untangle the Culprit knot with Reidemeister moves.2 Note that the first step increases the number of crossings before it can be untangled.
The main problem with this method is that we don’t know how long we need to continue before we simply give up. How do you know when to stop trying? There is no way to look at a knot and calculate the number of moves you need to transfer it from one to another state. All we know is that the theoretical maximum number of moves is unimaginably large and estimated to be $10^{2n10^{11}}$, where $n$ is the number of crossings.
In other words, if you take a complex unknot with lots of crossings and perform one random Reidemeister move per second, it could take much longer than a multitude of ages of the universe to get to a solution. Note that this unfathomably large number is the maximum number of random moves. With a bit of human intelligence, most unknots can be resolved much faster.
Unknotting algorithms
Reidemeister moves are a graphical and practical way to untangle mathematical knots. But the process requires some human insight and creativity. Mathematicians ask themselves how we can automatically solve the unknotting problem.
Wolfgang Haken devised an algorithm to tell if a knot projection is an unknot. His algorithm is so complicated, however, that it has never been implemented. Nevertheless, other mathematicians have worked on this problem and have developed different methods to automatically unknot a knot.
Knot theory is an exciting area of mathematics with new insights. For example, Oxford Mathematician Marc Lackenby has created an algorithm that determines whether a knot is the unknot in $n^{C \log{n}}$ steps, which is not quite as much as several ages of the universe.
In 1954 Alan Turing wrote "No systematic method is yet known by which one can tell whether two knots are the same."
— Oxford Mathematics (@OxUniMaths) February 2, 2021
In 2021, in a remarkable Gordian tour-de-force, Marc Lackenby reveals a new unknot recognition algorithm that runs in quasi-polynomial timehttps://t.co/0jGImTa9Uc pic.twitter.com/Y0n15Bu8DT
If you like to know about knot theory, then I highly recommend the lecture on the Mathematics of Knots by Jessica Purcell from the School of Mathematics at Monash University.
Unknot Diagram Hall of Fame
Knot theorists working on the unknotting problem have developed some fiendishly complex trivial knots to test their conjectures about the unknotting problem and their software.3
While these designs certainly have mathematical relevance and play a role in untangling the mysteries of the universe, the unknot can also be a thing of beauty. Complex unknots are inherently deceptive because they are not what they seem to be. Unknots are knots in disguise, and trying to untangle one in your mind can be challenging.
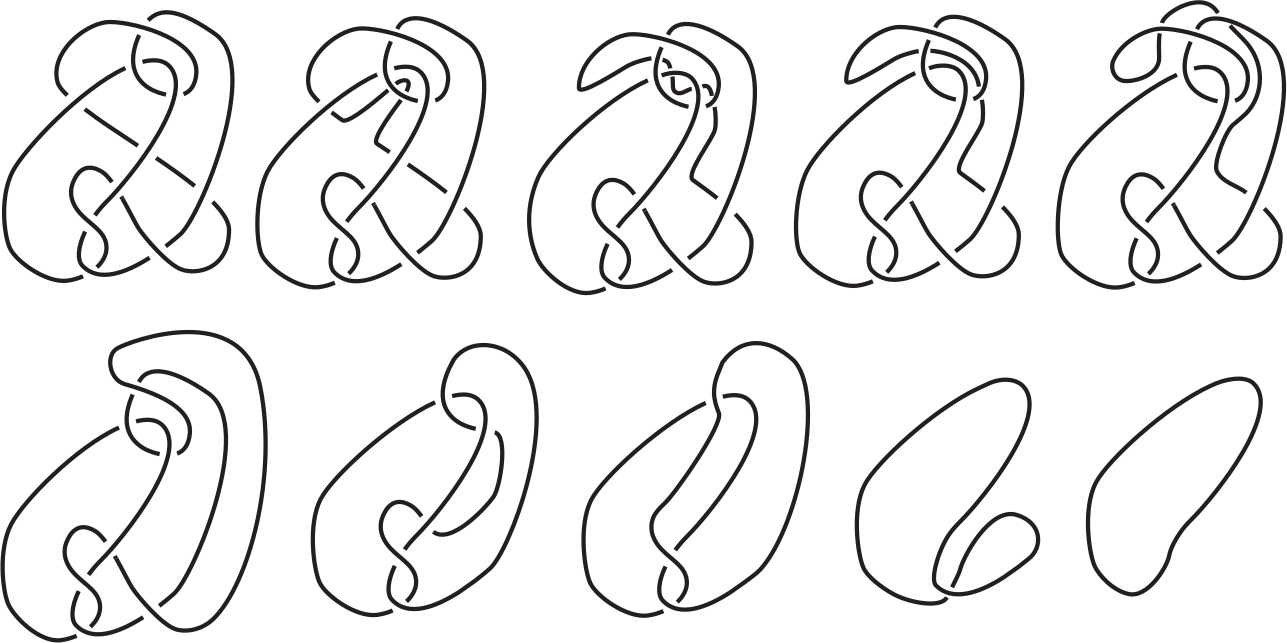
Goeritz
Lebrecht Goeritz was a German mathematician who designed some trivial knots almost a century ago. His most famous unknot has eleven crossings. The beauty of this knot is that you can extend the number of crossings by adding tangles on the left and right parts in the middle.
Thistlethwaite
Morwen Thistlethwaite is a knot theorist who made essential contributions to the field. He co-developed the Dowker–Thistlethwaite notation, which is a tool to encode knots for computers. He also defined a trivial knot with fifteen crossings that is often cited in the literature.
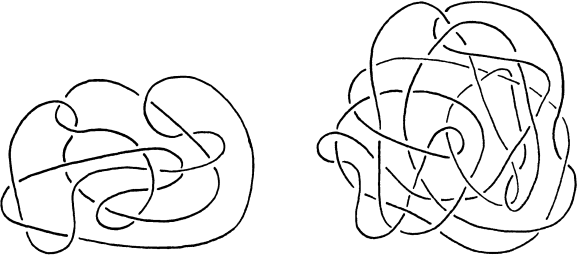
Ochiai
Japanese researcher Mitsuyuki Ochiai developed a computer program to decide the unknotting problem. He also constructed four complex trivial knots with an increasing number of crossings to test his theorems and software. The image below shows the first two of his creations.
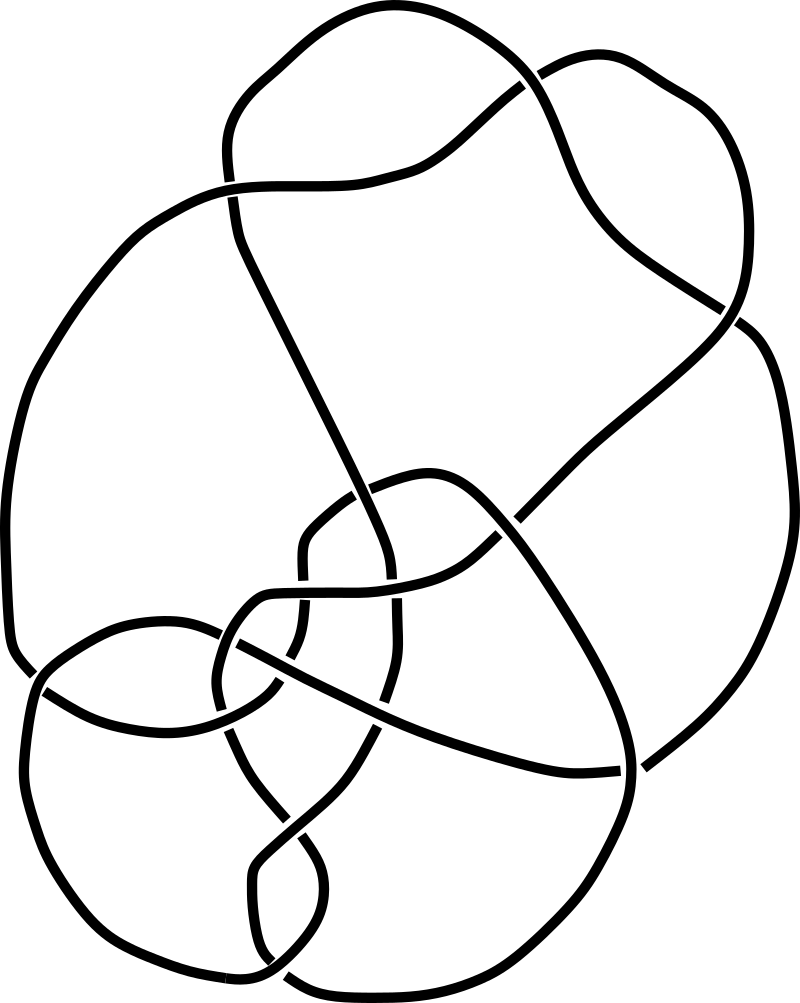
Haken
Wolfgang Haken developed the most complex trivial knots available in the literature. Haken is famous for co-solving the four-colour theorem, which states that any map can be filled with only colours so that no two adjacent regions have the same colour. You could also apply that theorem to his famous unknot shown below.

The name of this knot relates to a classic legend about the Gordian knot. Alexander the Great was challenged to untie the knot. The local legend said that whoever was able to undo it would rule Asia. Instead of using Reidemeister moves or carefully untangling the rope, he boldly cut it with his sword.
Unknots in Art
Knots have been part of human culture for tens of thousands of years. Humans of the early stone age used knots to create fishing nets and tie things together. Knots are not only practical; they also feature in the arts. We find images of knots in the art of cultures around the globe and through the ages.8
The traditional sand drawings of Vanuatu, which I discussed in a previous article, look like geometric projections of knots. Most designs are drawn with a finger in the sand in one continuous line. Because the finger does not leave the sand, these designs are trivial knots.
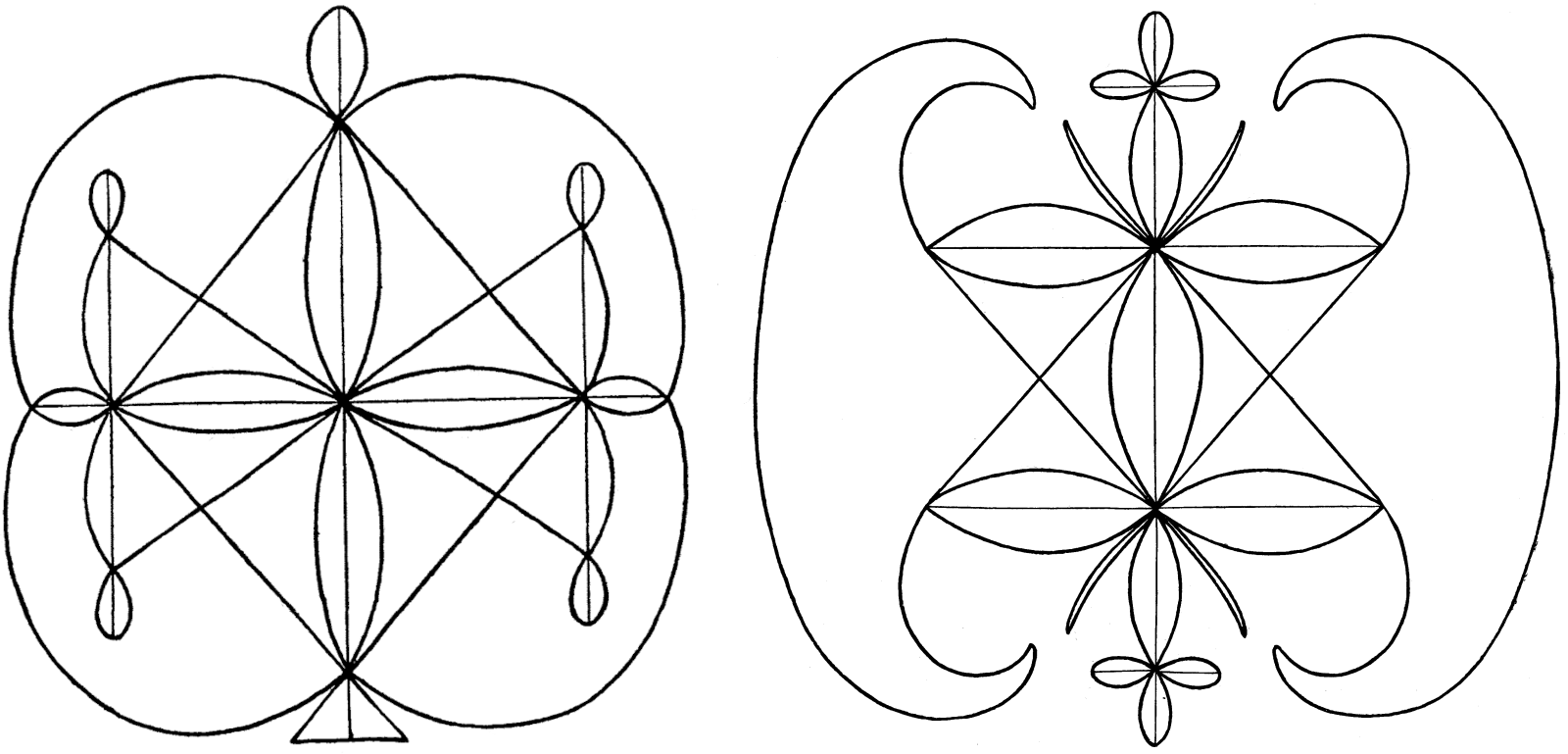
The unknot has inspired not only mathematicians but also visual artists. For example, abstract painter James Sienna painted some works inspired by the unknot. Whether these designs are actually trivial knots remains to be seen.
Mick Burton is a continuous line artist, which means he draws pictures in one continuous line. Mick found inspiration in knot theory and Haken’s Gordian Knot in particular, which produced this wonderful painting. He also devised a method to construct Haken's Gordian Knot, which was the basis of the above animation.

Magical Unknotting
Magicians love to use ropes and knots to create the illusion of magic. The Conjuring Archive lists hundreds of effects that involve knots. Most of these either cause knots to appear or dissolve.
A dissolving knot is a trick where a magician appears to tie a genuine knot, but it melts away. These types of tricks are unknots in motion. Magicians have developed a range of techniques to tie an unknot.
This video by magician Doug Conn teaches a short knot routine that shows how to tie the two most common dissolving knots.
Dissolving knots are deceptive because, in our experience, every tangled mess of rope is knotted. Unfortunately, we cannot determine whether a piece of rope is knotted by merely looking at it. The complexity of the unknotting problem in mathematics supports this intuition.
Just like mathematical unknots, dissolving knots are named after the person who composed them. The two most famous versions are the Chefalo knot and the Hunter Bow Knot, which Doug teaches in his video.
Magic and topology often go hand-in-hand as a myriad of tricks uses topology either as a method or as a plot. Famous knot theorist Louis Kaufman loves to perform knot magic tricks in his lectures.
So let’s treat these two dissolving knots the same way as the mathematical projections we seen above. First, I created the knots, connected the ends and laid them out on the table before dissolving them. I then photographed the ropes and drew the projection.
The resulting diagrams show the projections of the Chefalo Knot (11 crossings) and Hunter Bowknot (9 crossings). You can also combine these knots by tying the Chefalo Knot on top of the bowknot, which gives an unknot with 20 crossings.
Perhaps a mathematician reading this page can work out the proof that these are indeed trivial knots without pulling the ends.
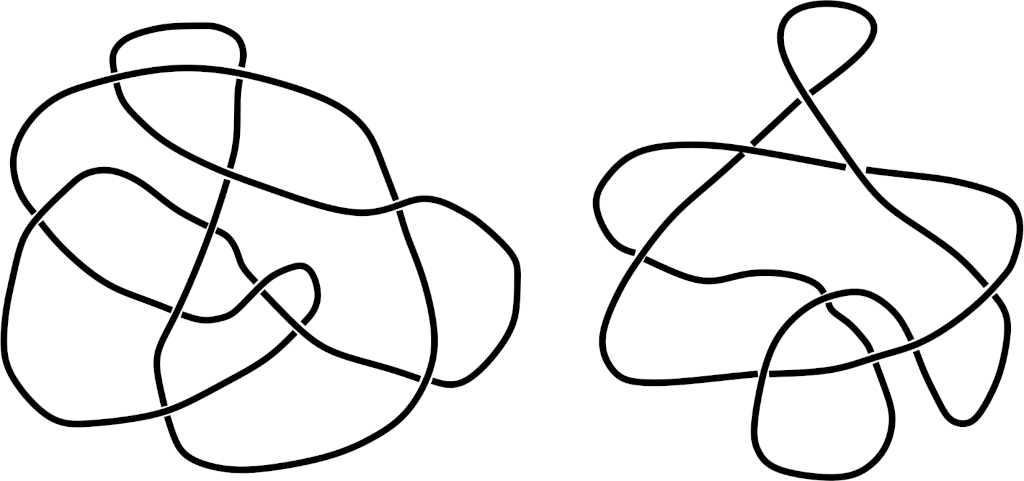
An Ode to the Unknot
This ode to the unknot shows that it is by no means trivial. On the contrary, the unknot hides a deep mathematical complexity and has inspired both artists and magicians.
Complex trivial knots are deceptive because they look more elaborate than they are. So next time you are stuck with a tangled garden hose, don’t panic but find the unknot that hides within. Perhaps the more important lesson is that no matter how tangled up your life is, there is a way to simplify the situation.
Feel free to contact me or leave a comment below if you have any additions to my collection of unknots.

Notes
Adams, C. C., The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots (1994), New York: W.H. Freeman.
Henrich, A., & Kauffman, L. H., Unknotting Unknots, The American Mathematical Monthly, 121(5), 379 (2014) DOI 10.4169/amer.math.monthly.121.05.379.
Burton, B. A. et al.Hard diagrams of the unknot, (2021). arXiv:2104.14076.
Kauffman, L. H., & Lambropoulou, S., Hard unknots and collapsing tangles, Series on Knots and Everything, 187–247 (2011) DOI 10.1142/9789814313001_0009.
Petronio, C., & Zanellati, A., Algorithmic simplification of knot diagrams: New moves and experiments (2016). arXiv:1508.03226v3.
Ochiai, M., Nontrivial projections of the trivial knot, Astérisque, 192, 7–10 (1990).
Stewart, I., Professor Stewart’s Cabinet of Mathematical Curiosities (2008), London: Profile Books.
Jablan, S., Radović, L., Sazdanović, R., & Zeković, A., Knots in art, Symmetry, 4(2), 302–328 (2012) DOI 10.3390/sym4020302.
Deacon, A. B., & Wedgwood, C. H., Geometrical Drawings from Malekula and Other Islands of the New Hebrides, The Journal of the Royal Anthropological Institute of Great Britain and Ireland, 64, 129–175 (1934) DOI 10.2307/2843952.
Share this content


