Topological Magic Tricks: Shapes as a Method for Deception
Peter Prevos |
615 words | 3 minutes
Share this content
Magicians often use the principles of science as a method to create the illusion that real magic has occurred. Most tricks that use mathematics, such as the many card routines, rely on number theory through counting and sorting patterns. Some magic tricks, such as the enigmatic vanishing square puzzles, use principles of geometry. A small subgroup of scientific magic is topological magic tricks both as a method and as a plot.
What is topology?
The word topology was first introduced by the 19th-century German mathematician Johann Listing. He is also known for simultaneously discovering what is now known as the Möbius strip. Topology is a branch of mathematics concerned with the (logos) of space (topos).
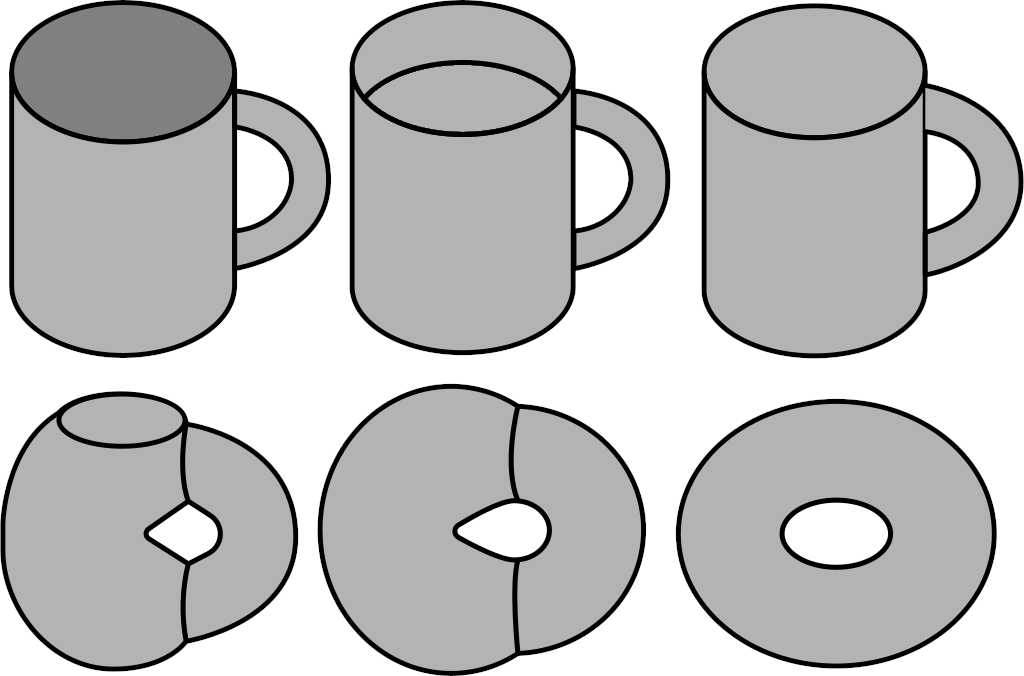
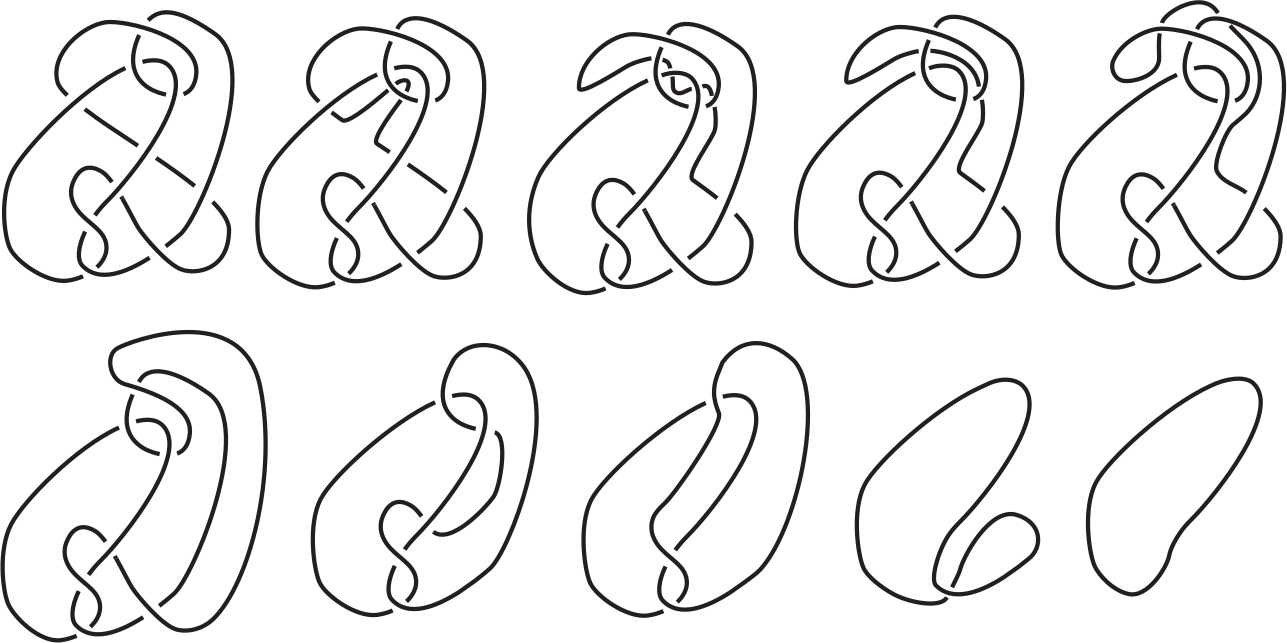
Mathematicians involved with topology study transform into other shapes. To a topologist, a doughnut made from silly putty is equivalent to a coffee mug because one can be transformed into the other without drilling holes or adding material. Another favourite past time of topologists is the study of knots. One of the significant problems in knot theory is determining whether a knot is actually a knot or just a tangled mess.
Topology is an artful and speculative branch of mathematics, but it also has many practical applications. Topology is an essential input into many technologies we rely on, such as the internet. This form of mathematics also plays a role in physics and biology. Lastly, topology can be used to create the illusion of magic.
Topology is the silly putty of mathematics.
Topological magic tricks
Topology appears in magic as an effect as a method. Basically, all rope tricks are topological effects. Most tricks with rings involve linking and unlinking them by melting metal through metal. Linking ring tricks feign to violate a principle of topology which states that two closed curves cannot link or unlink without breaking them apart. Magic books also describe a lot of fake knots, within the vocabulary of topology are unknots.
Topology as a Method
The most famous of all topological magic tricks is the Afghan Bands. This trick uses the Möbius Strip as a technique to create magic. The primary effect is that a loop is cut or ripped in half with unexpected consequences.
The Möbius Strip is a two-dimensional loop that paradoxically only has one side. This principle has been studied by magicians, used by inventors and has inspired artists since it was first discovered. Magicians have performed this trick for over a century with paper, cloth and with zippers.
The video below shows Harry Blackstone performing his version with cloth bands which he called the Red Rags.
The Möbius Strip in Magic: A Treatise on the Afghan Bands
Magicians use the Möbius strip to perform magic under the name Afghan Bands. This ebook describes the principles, history and performance this topological trick.
Topology as a Plot
All rope tricks are essentially topological magic tricks. Magicians cut and restore ropes and magically tie or untie knots. In knot theory, a branch of topology, knots can be deformed in any way, except by cutting the cord. Magic tricks thus don't use topology but appear to be topological while
In knot theory, all knots are shows as loops. One of the essential questions in knot theory is a loop is a knot or knot. Mathematicians call a loop that has no knot an unknot. Some of these fake knots are quite complex and look like real knots. Magicians know various ways to apparently knot a rope and magically dissolve it into an unknot.
Share this content
