Geometric Magic Tricks: Conjuring with Size and Geometry

The Gozinta Boxes are a famous example of magic with geometry. The basic effect is a topological mystery where two boxes fit inside each other. The method for this trick is not topology, but a clever application of geometry. Lubor Fiedler discovered the principle behind the gozinta box when tidying his house. He placed two empty boxes into each other and noticed how they seemed to fit into each other almost perfectly. This real-life situation inspired him to develop the Lubor Die, which later became known as the Gozinta Boxes.

A Gozinta Box consists of two hollow cubes with perceived rib size a and wall thickness $t$. We can use mathematics to prove that a gozinta box is magical. The following equation ensures that the boxes fit into each other: $a^3 = (a - t)^3$. This formula expresses symbolically that the volume of the outside of the cube $a^3$, is equal to the volume of the inside of the cube: $(a - t)^3$ . This equation is only valid when either the wall thickness $t = 0$, or when the rib length approaches infinity, a $\rightarrow \infty$.

The absurdity of zero wall thickness or infinite cube size expresses the magical quality of the gozinta box. When the wall thickness is zero, the boxes consist of only space and imaginary boxes will naturally fit perfectly into each other. Cubes of infinite size are magical because they are simply beyond contemplation.

If you like to know everything there is to know about Gozinta Boxes, then consider purchasing The Box Goes-In-Da Box ebook. When you subscribe to the Horizon of Reason magic newsletter, you get a free copy of the Gozinta Box Construction Kit with a template and instructions to create Gozinta boxes.

A geometric vanish is a situation where a set of tiles can create two shapes with apparently different surface areas. There are three types of geometric vanishes that magicians can use to create the illusion of magic.

• Vanishing Leprechaun
• Curry Paradox
• Tangram Paradox

Each of these creates a similar effect but uses slightly different mathematical principles.

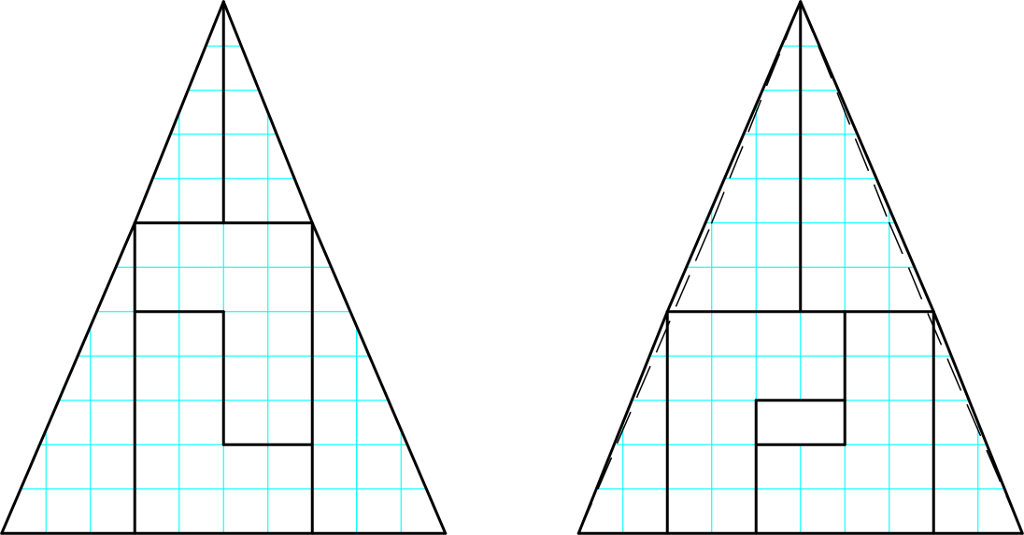
Curry Paradox

The Curry Paradox is similar to the Tangram paradox but in this puzzle, the pieces don't have the same angles. The illustration shows the Curry Triangle. In this version, a triangle is cut into pieces and when the pieces are moved, the triangle has the same area, but two squares are missing.

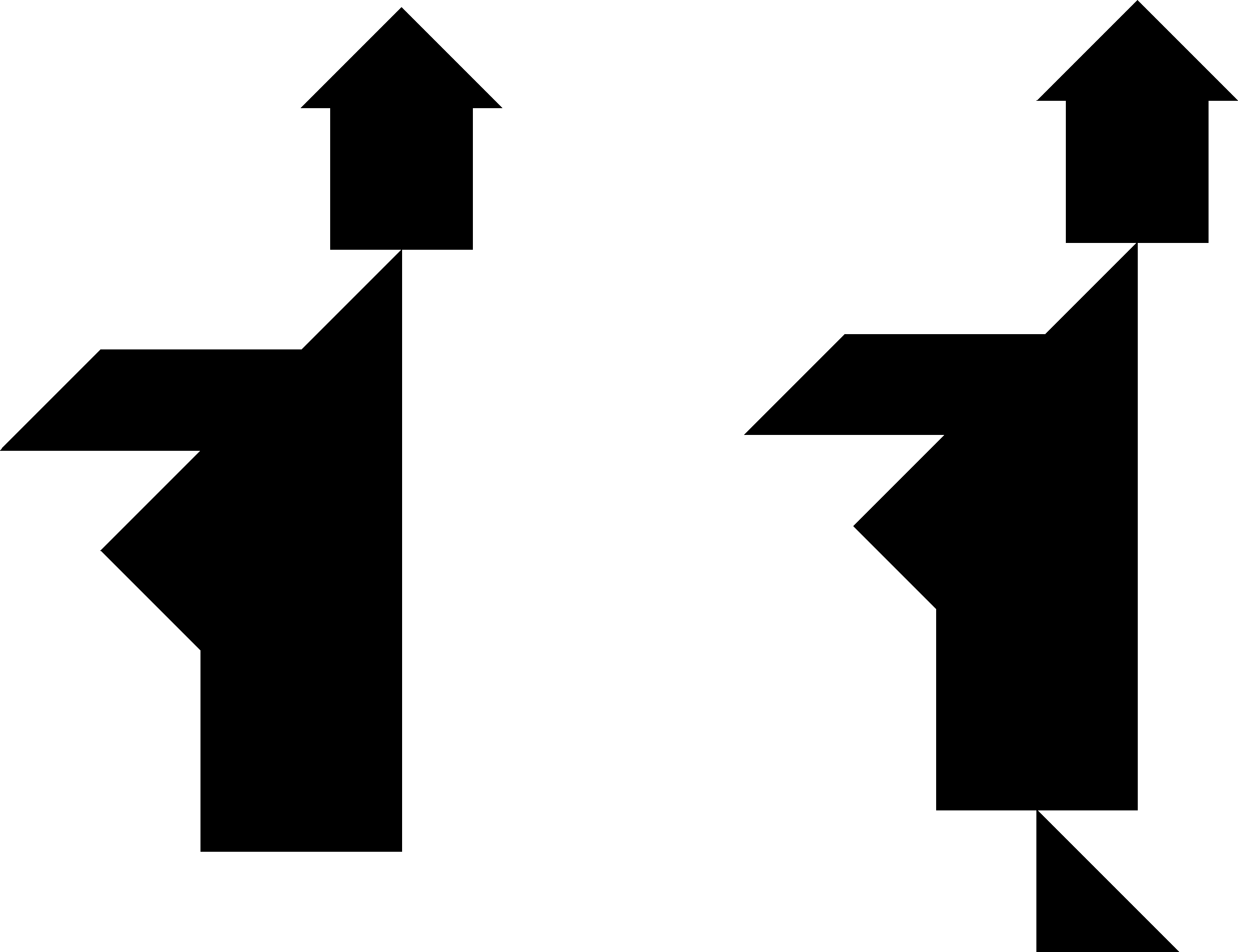
Tangram Paradox

Tangram is an old Chinese puzzle used to compose images using seven geometrical tiles. An apparent paradox occurs when two equal shapes are created using all seven tiles, but one is smaller than the other. The image shows the famous paradox of two monks. A magical implementation of the Tangram paradox in magic is Paradox by Mitsonubu Matsuyama.

If you like to know everything about Geometric Vanishes, then you need to read Paradoxes of Size: A Treatise on Geometric Vanishes.